1. INTRODUCTION
1.1 DEFINITION
Definition |
-Incoming solar radiation is the intensity of incoming solar radiation on an object.
Incoming Solar Radiation (Eo)   Ref: Ahrens 2007
-Typical Units are Wm-2 (Flux/Unit Area)
Measures solar input on a horizontal surface. |
1.2 KEY FACTS
Insolation Varies Depending on: |
-Time of Year
-Solar Declination
-Earth-Sun Distance
-Latitude
-Time of day (solar zenith)
-Atmoshperic Conditions (Clouds, smoke, pollution, diffuse sky light |
Important Relationships Include: |
Important Relationships:
Lamberts Cosine Law: Eθ=Eo cos(θ)
Beer-Lambert Law: Eθτ=Eθ*e^ (- τ n*m)
τ n = normal optical thickness
m = airmasses (1/cos(θ))
Other impacts on τ
– elevation: τh= τ0e^(-z/8.434km) |
General Facts: |
- Represents input solar energy into the system
- Rsw = incoming – outgoing
- Incoming = Insolation*(1-albedo), where albedo=fraction of incident radiation
that is reflected (value between 0 and 1, e.g. snow ~= 0.9 and grass ~= 0.3)
- Outgoing = Insolation*albedo
- Drives numerous physical and biological processes
- Absorbed energy heats the surface and air
- Diurnal variation controls surface and air temperatures
- Seasonal variation influences weather
- Latitudinal variation is a major control on climate
- Absorbed Photosynthetically Active Radiation drives photosynthesis while
the full spectrum drives Evapotranspiration
- Alternate units: Mole, or Mole/m2/sec
- Daylight Length (Photoperiod)
- Environmental cue used by plants
|
2. RELATED MATERIAL
2.1 SOLAR INTENSITY
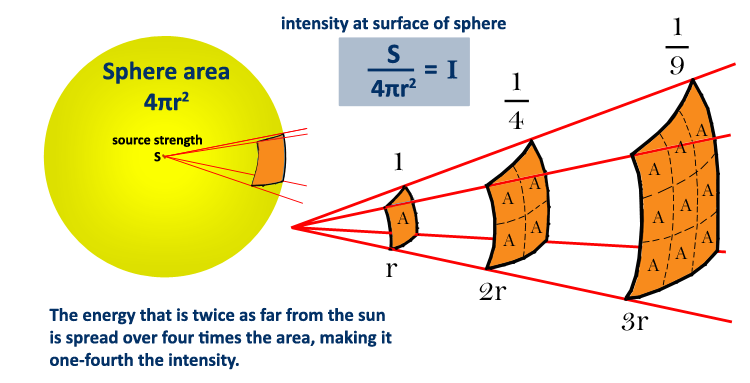
Solar Intensity
Solar intensity changes with distance.As distance is doubled, for example, the energy is spread over four times the area. This results in an intensity that is one-fourth its original strength.
|
|
2.2 THE SOLAR SPECTRUM
The Solar Spectrum
Insolation is primarily short wave radiation: 350 to 3000 nm, and 50% of
this energy is in the visible portion of the spectrum..
|
|
2.3 SOLAR DECLINATION (δ)
|
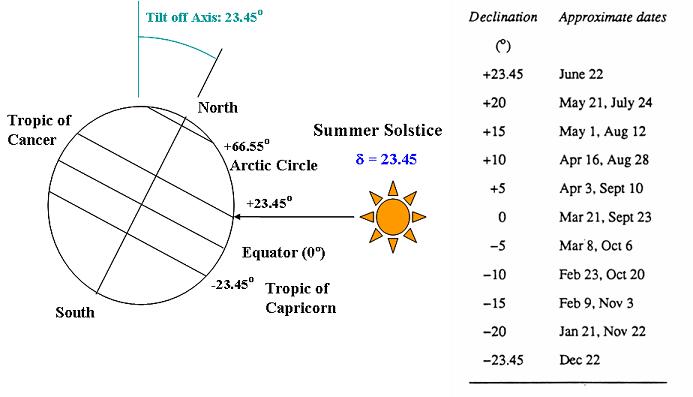
Solar Declination (δ)
-Earth's axial tilt is: 23.45º
-Solar Declination = Latitude of the subsolar point (where the sun is directly
overhead at solar noon)
-Solar Declination (δ) changes seasonally, and is calculated by the day of year using the following equation:
| δ =23.45*cos(2*π*(JD-172)/365) |
Where:
JD = Julian Day (count the days from Jan.1st)
Solar
dec. calculator
|
|
2.4 SEASONS
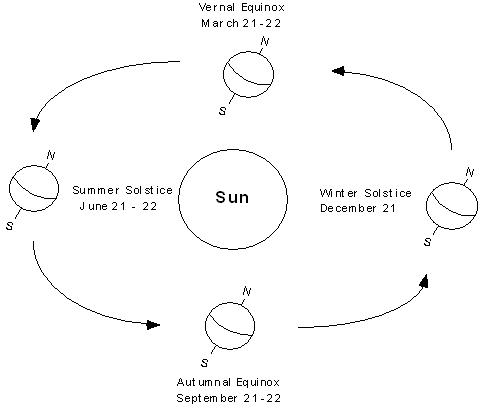
Seasons
- Describes the revolution of the Earth around the Sun
- Orbital tilt causes changes in the position of sun and local incidence
- Controls seasonal changes in solar zenith
- Controls seasonal changes in irradiance
- Controls daylight length
- Accounts for our four basic seasons
|
|
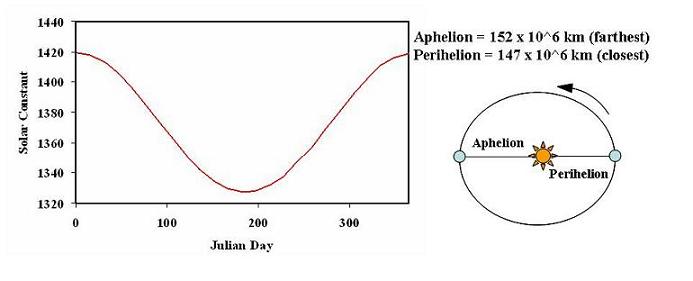
2.5 SUN-EARTH DISTANCE
Sun-Earth Distance
The sun and earth are closest during perihelion and farthest away during
aphelion. The Solar constant is the incoming solar radiation measured
at the top of the Earth's atmosphere on a surface that is perpendicular
to the incident rays. While the average is 1367 W/m2, it varies due to
the earth-sun distance, since radiation intensity is proportional to the
square inverse of the sun-earth distance. This is because the surface
area (4*pi*r^2) over which the sun's energy is distributed will increase
with r, the earth-sun distance, and therefore since the total energy is
constant, the intensity (W/m2) must decrease.
|
E TOA = M*(4*PI*Rs 2)/(4*PI*Reo 2)
E TOA = Irradiance at the top of the Earth's atmosphere
M = Irradiance (Exitance) at the surface of the Sun
Rs = Radius of the sun
Reo = Radius of the earth's orbit (earth-sun distance)
|
2.6 THREE ORBITAL PARAMETERS OF MILANKOVITCH
Three Orbital Parameters of Milankovitch
1. Precession: Changes the timing of when the Earth is closest to the
Sun
Current Configuration:
- Perihelion (closest): December
- Aphelion (farthest): June
- Northern hemisphere has warmer winters, cooler summers than
Southern hemisphere
|
PRECESSION
 |
2. Obliquity: (Axial Tilt) Changes the severity of the seasons
- 21.5 degrees, least extreme
- 24.5 degrees, most extreme
|
OBLIQUITY
 |
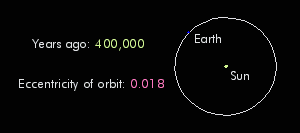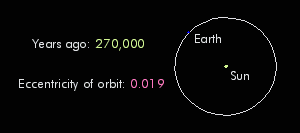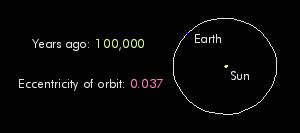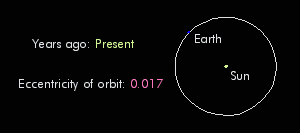
3. Eccentricity: Changes the overall radiation balance of Earth
- Eccentric: Most variable
- Least Eccentric: Least variable
Images from Dylan Parenti 2008
|
ECCENTRICITY
 |
2.7 INSOLATION AND LATITUDE
Insolation and Latitude
- Insolation decreases with increased latitude
- Eθ=E0cos(θ)
- θ=|β-δ|
|
|
2.8 DIURNAL INSOLATION
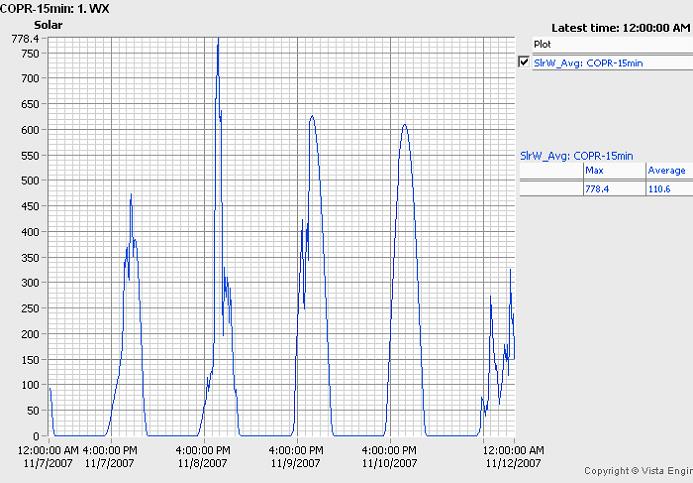
Comparison of measured insolation at Coal Oil Point on December
22 to modeled insolation with and without an atmosphere 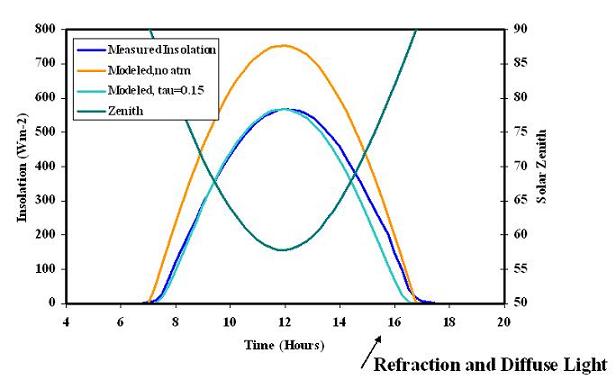
|
Diurnal Insolation
- Varies with Solar Zenith
- Varies with Direct vs Diffuse Beam
- Peaks at Solar Noon
- What is solar noon?
- When does it occur?
- Solar Zenith (θsun)
- cos θsun=sin(δ)sin(β)+cos(δ)cos(β)cos(ω-λ)
- Solar Azimuth(phi;sun)
- tanφsun=cos(δ)sin(ω-λ)/(cos(δ)sin(β)cos(ω-λ)-sin(δ)cos(β))
- Where,
δ = solar declination
ω= solar longitude
β = observer latitude
λ = observer longitude
ω-λ = hour angle
|
2.9 DAYLIGHT LENGTH (PHOTOPERIOD)
Daylight Length (Photoperiod)
-
Varies primarily as a function of latitude and solar declination
- DLL = 2*cos-1(-tan(δ)*tan(β))* hr/15º
-
Photoperiod is a major environmental cue used by plants to time germination,
leaf drop and prepare for winter (cold hardiness)
-
Sunrise: SN -(ω-λ)*hr/15°
-
Sunset: SN + (ω-λ)*hr/15°
|
|
2.10 SOLAR NOON AND THE EQUATION OF TIME
|
Solar Noon and the Equation of Time
|
2.11 ATMOSPHERIC IMPACTS
Atmospheric Impacts
- The atmosphere absorbs and scatters shortwave
- Absorption reduces direct beam radiation
- Scattering reduces direct beam, adds diffuse beam
- The atmosphere absorbs and reemits longwave
|
|
2.12 NORMAL OPTICAL THICKNESS
NORMAL OPTICAL THICKNESS
Quantifies attenuation by scattering and absorption
- E = E0e-(α+β)*pathlength
- α = absorption coefficient
- β = scattering coefficient
- Combined, α+β attenuate light
- In an atmosphere we need to weight attenuation by absorbers and scatterers
by the change in particle density with height
- We call that weighted extinction coefficient normal optical thickness
(τ)
- Esurf = E0e-τ
|
|
2.13 OPTICAL THICKNESS & ATMOSPHERIC SPECIES
Optical Thickness & Atmospheric Species
|
|
WATER VAPOR (unique in that it varies considerably over space and time)
|

|
2.14 AIR MASSES
Air Masses
How do you relate pathlength to zenith angle?
Pathlength = 1/cos(θ) = airmasses (m) |
|
3. INSTRUMENTATION
3.1 PYRONOMETER
Instrumentation
Other Measures of Light:
- Diffuse light (Diffuse=Total - Direct)
- Block out direct beam with a shadowband
- Highest early or late in the day or in overcast or partially overcast
conditions
- PAR: Photosynthetically Active Radiation
- Restricted to 400 to 700 nm
- Sensitivity weighted to compensate for variable photon energy
- Units (Moles of Photons), 1 mole = 6.02x1023 photons
- PPFD: Photon Flux Density
- Restricted to 400 to 700 nm
- Photons per unit area and time (moles/m2/sec)
|

Pyranometer at Coal Oil Point Reserve, Photo by Dar Roberts; July 18, 2007.
LI200X
Silicon Pyranometer
The LI200X Silicon Pyranometer is used to accurately measure sun plus
sky radiation in the 400 to 1100 nm waveband. It is used extensivly in
solar, agricultural, and meteorological applications.
The sensor includes diffuser, cosine correction and level bubble. It should
be nstalled in a location where it will not be shaded (such as the south
end of tower crossarm). Installed at: COPR, Airstrip, Lisque |
4. LOCAL INSOLATION CHARTS
4.1 INSOLATION CHART EXAMPLE
Time: UTC
Units: Watts/m2
|
|
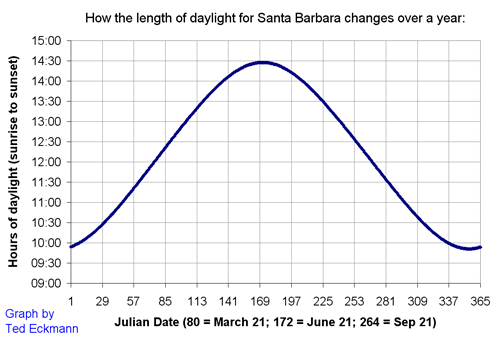
4.2 ANNUAL DAYLIGHT, SUNSET, AND SUNRISE TIMES FOR SANTA BARBARA
Place cursor over text to view each chart. Click text to view larger version in a new window. |
 |
|
|
Click here for a Julian Date Conversion Table (pdf)
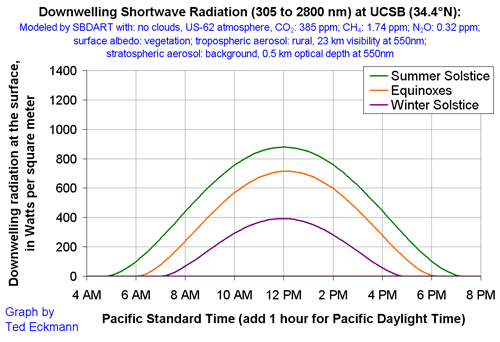
4.3 DOWNWELLING SHORTWAVE RADIATION AT THE SURFACE AND TOP OF
THE ATMOSPHERE AT UCSB
Return to Home Page